Soal 11. SIMAK UI/2012/521/29
Dinding berbentuk huruf "v" dibangun dari dua bidang miring identik tanpa gesekan. Jika benda bermassa m mula-mula diletakan pada salah satu bidang miring tersebut, maka benda akan melakukan gerak harmonis sederhana.
Sebab
maka, jawabanya
(a) pernyataan benar, alasan benar, dan keduanya menunjukkan hubungan sebab dan akibat.
(b) pernyataan benar, alasan benar, tetapi keduanya tidak menunjukkan hubungan sebab dan akibat.
(c) pernyataan benar dan alasan salah.
(d) pernyataan salah dan alasan benar.
(e) pernyataan dan alasan keduanya salah.
Jawab: Perhatikan gambar berikut sebagai visualisasi.
Cek pernyataan 1.
Syarat gerak harmonik adalah energi mekanik objek konstan/ tidak berkurang. Selama bergerak di permukaan dinding, bola memang tidak mengalami pengurangan energi (karena licin), namun saat bertumbukkan dengan dinding bawah energi mekanik bola bisa tetap atau berkurang tergantung jenis tumbukannya. Karena di soal tidak dibatasi jenis tumbukkanya, maka energi mekaniknya belum tentu konstan, artinya belum tentu terjadi gerak harmonik sederhana. \(\Rightarrow\) pernyataan 1 salah.
Cek pernyataan 2.
masih berkaitan dengan penjelasan pernyataan 1. Karena energi mekaniknya belum tentu konstan, artinya belum tentu juga tinggi pantulan akan sama dengan tinggi mula-mula. \(\Rightarrow\) pernyataan 2 salah.
(Jawaban e.)
Soal 12. SIMAK UI/2012/521/30
Usaha yang dilakukan oleh gaya konservatif pada benda hanya bergantung pada posisi awal dan akhir benda itu saja, tidak bergantung pada lintasan yang dilaluinya.
Sebab
Gesekan membuat energi mekanik akhir suatu benda selalu lebih kecil dari eneri mekanik awal benda tersebut. (pilihan jawaban sama dengan soal 11.)
Penyelesaian:
Cek pernyataan 1.
Ditinjau dari usaha yang dihasilkan, gaya dibagi atas: gaya konservatif dan gaya non konservatif.
contoh gaya konservatif: gaya berat, gaya pegas, gaya coulomb, dan gaya magnet.
contoh gaya non konservatif: gaya berat, gaya pegas, gaya coulomb, dan gaya magnet.
Lihat gambar berikut!
Gambar di atas memperlihatkan sebuah troli mini bermassa \(m\) digerakkan melalui rel melingkar ABCD. Mari tinjau usaha yang dihasilkan oleh gaya berat dan usaha gaya gesek dari kasus gerak troli ini.
Jika A adalah kondisi awal dan D adalah kondisi akhir, maka usaha yang dilakukan gaya berat \(Ww\) dari titik A ke D melalui lintasan ABCD adalah sama dengan usaha yang dilakukan gaya berat \(Ww\) melalui lintasan AD, atau:
\(Ww_{ABCD} = Ww_{AD} = -\Delta EP\)
Di mana:
\(-\Delta EP\ = - m.g.\Delta h = -m.g.R\)
Lain halnya dengan usaha gaya gesek. dengan asumsi kondisi awal dan akhir yang sama, maka usaha gaya gesek (\(W_{fges}\) ) melalui lintasan ABCD > dibandingkan usaha gaya gesek melalui lintasan AD, atau:
\(W_{fges_ABCD} > W_{fges_AD}\)
Hal tersebut dikarenakan jalur ABCD lebih banyak produksi panas/ kalor (akibat gaya gesek) dibandingkan dengan jalur AD langsung.
Berdasarkan contoh dua kasus gaya tersebut disimpulkan bahwa usaha gaya konsevatif (gaya berat) hanya bergantung kondisi awal dan akhir, tidak bergantung bentuk dan/ panjang lintasan. sedangkan usaha gaya non konservatif nilai bergantung bentuk/ panjang lintasan yang dilalui benda. \(\Rightarrow\) pernyataan 1 benar.
Cek pernyataan 2.
Efek yang ditimbulkan oleh adanya usaha gaya gesek adalah :
1. timbul panas
2. gerak benda melambat, (energi mekanik sistem berkurang)
\[W_{fges} = -\Delta EM\]
\(\Rightarrow\) pernyataan 1 benar.
Pernyataan 1 dan 2 benar, namun tidak menunjukkan hubungan sebab akibat \(\Rightarrow\) (jawaban b.)
Soal 13. SIMAK UI/2012/521/32
Sebuah benda yang massanya 2,00 kg bergetar harmonis sederhana dengan persamaan simpangan, \(y=0.20 sin (45t)\) dalam satuan S1, maka....
I. pada saat t= 2 detik simpangannya = 0,20 m
II. pada saat t= 4/3 s. Kecepatannya = 0,10 m/s
III. energi kinetik maksimumnya = 81,00 J
IV. energi total benda = 9,00 J
Pernyataan yang benar adalah ....
a. I, II, III D. IV saja
b. I dan III E. semua benar
c. II dan IV
Diketahui:
\(m = 2\) kg
\(y=0.20 sin (45t)\) m
Cek pernyataan I.
\(y = 0,20 sin(45\times 2)\)
\(y = 0,20 \times 1\) = 0,20 m (betul)
Cek pernyataan II.
\(v = {dy\over dt}\)
\(v = 0,2\times 45 .cos (45.t)\)
\(v = 9 .cos (45.t)\)
\(v = 9.cos (45\times {4\over3})\) \(\Rightarrow\) \(t = {4\over3}\) s
\(v = 9.cos (60)\)
\(v = 9\times {1\over 2} = 4,5\) m/s (salah)
Cek pernyataan III
\(EM = Ek_{maks} = {1\over2}.m.v_{maks}{2}\)
\(v_{maks} = 9\times cos (0) = 9 \) m/s
\(EM = {1\over2}\times 2 \times 9^2 = 81\) Joule (benar)
Cek pernyataan IV.
\(Ek_{maks}\) = 9 J (salah) (lihat Cek pernyataaan III)
(Jawaban I dan III benar \(\Rightarrow\) b)
SOAL 14 SIMAK UI 2013/235/26
Sebuah balok ditembak pada arah vertikal dengan sebuah peluru yang memiliki kecepatan 500 m/s. massa peluru tersebut 10 gr, sedangkan masa balok 2 kg. Setelah ditembakkan, peluru bersarang di dalam balok. Balok akan terpental ke atas hingga ketinggian maksimum ....
a. 13 cm d. 42 cm
b. 27 cm e. 47 cm
c. 31 cm
Diketahui:
\(m_p = 10 gr = 0,01\) kg\(m_b = 2\) kg
\(v_p = 500\) m/s
Ditanyakan: \(h_{maks} =\) ....?
Jawab: Perhatikan gambar berikut!
Untuk kondisi 1 dan 2: berlaku hukum kekekalan momentum, yaitu:\(\Sigma p_{awal} = \Sigma p_{akhir}\)
\(p_p + p_b = p'_p + p'_b\)
\(m_p.v_p + m_b.v_b = m_p.v'_p + m_b.v'_b\)
 |
| Kondisi 1: sesaat sebelum peluru menumbuk balok, kondisi 2: sesaat setelah peluru bersarang di dalam balok, kondisi 3: kondisi balok dan peluru mencapai tinggi maksimum. |
Untuk kondisi 1 dan 2: berlaku hukum kekekalan momentum, yaitu:
\(p_p + p_b = p'_p + p'_b\)
\(m_p.v_p + m_b.v_b = m_p.v'_p + m_b.v'_b\)
\(\Rightarrow v_b = 0\), \(v'_p = v'_b = v'\)
\(m_p.v_p = (m_p + m_b).v'\)
\(v' = {m_p.v_p\over m_p + m_b}\)
\(v' = {0,01.500\over 0,01 + 2}\)
\(v' \approx 2,5\) m/s
Untuk kondisi 2 dan 3: bisa digunakan persamaan Gerak Vertikal ke Atas berikut:
\(v_t^2 = v_0^2 - 2.g.h\)
saat \(h = h_{maks } \Rightarrow v_t = 0\), sehingga:
\(0 = v_0^2 - 2.g.h_{maks}\)
\(h_{maks} ={v_0^2 \over 2.g}\)
dengan:
\(v_0 = v' = 2,5\) m/s dan \(g = 10\) m.\(s^{-2}\)
\(h_{maks} ={2,5^2 \over 20}\) m
\(h_{maks} ={625 \over 20}\) cm
\(h_{maks} \approx 31\) cm \(\Rightarrow\) (Jawaban c.)
Soal 15. SIMAK UI 2013/235/34
SEBAB
(Pilihan jawaban sama dengan soal 11.)
Jawab:
Cek Pernyataan 1.
Usaha total untuk memindahkan benda (termasuk gerak menggelinding) di bidang horizontal sama dengan perubahan energi kinetiknya, atau:
\(W_{total} = \Delta Ek = {1\over 2} m.(v_t^2 - v_0^2)\)
Karena roda menggelinding dengan kecepatan linier konstan. artinya \(v_t = v_0 \), maka:
\(\Delta Ek = 0 \Rightarrow W_{total} = 0\) \(\Rightarrow\) (Pernyataan 1 betul)
Cek Pernyataan 2.
Rumus usaha \(W = \Sigma F_x.\Delta x\), \(F_x =\) gaya (N), \(\Delta x =\) perpindahan (m), (pernyataan 2 betul)
Pernyataan 2 menunjukkan hubungan sebab akibat dengan pernyataan 1. (jika \(\Sigma F = 0 \Rightarrow \) laju konstan \(\Delta Ek = 0 \Rightarrow W = 0\)
(Jawaban A)
Soal 16 SIMAK UI/2014/302/25
Tiga pegas identik (k = 200 N/m) dan dua beban (massa masing-masing = 0,5 kg) disusun seperti pada gambar. Pertambahan panjang total pegas adalah ....
a. 4,0 cm d. 7,0 cm
b. 5,0 cm e. 8,0 cm
c. 6,0 cm
Penyelesaian. Soal tentang elatisitas. Untuk menentukan pertambahan panjang dapat digunakan Hk. hooke, yaitu:
\(F = k.\Delta L\) \(Rightarrow \Delta L = {F\over k}\)
sementara \(F\) diperankan oleh berat beban \(w = m.g\), sehingga:
\(\Delta L = {m.g\over k}\) .... (16.1)
Perhatikan gambar berikut:
Dua pegas saling paralel dapat digantikan dengan pegas pengganti dengan konstanta \(kp\), di mana:
\(kp = k + k = 2k = 400\) N/m
Pegas kp ini menanggung dua beban \(Mp = m_1 + m_2 = 2m = 1 kg\). Sedangkan pegas k di bawah \(m_1\) hanya menanggung \(m_2 = 0,5\) kg.
untuk pertambahan panjang sistem pegas ini, merupakan penjumlaha pertambahan panjang yang dialami pegas kp dan pegas k. atau:
\(\Delta L = \Delta L_p + \Delta L_k\)
dengan menggunakaan persamaan (16.1), maka:
\(\Delta L = {2m.g\over 2k} + {m.g\over k}\)
\(\Delta L = {2m.g\over k} = {2.0,5.10\over 200}\) m
\(\Delta L = 0,05\) m = 5,00 cm \(\Rightarrow\) (jawaban b.)
Soal 17. SIMAK UI 2014/302/26
a. 0,2 d. 0,8
b. 0,4 e. 0,1
c. 0,6
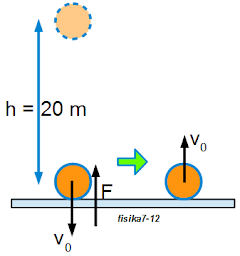
Penyelesaian. Perhatikan gambar berikut.
Untuk menentukan koefisien restitusi pada peristiwa benda jatuh dapat menggunakan persamaa berikut:
\(e = {-v_t\over v_0}\) .... (17.1)
\(v_0\) dapat ditentukan dengan menggunakan rumus kecepata gerak jatuh bebas
\(v_0 = - \sqrt{2.g.h}\)
\(v_0 = - \sqrt{2.10.20} = - 20\) m/s
(tanda - karena arahnya ke bawah)
untuk \(v_t\) dapat digunakan dengan hubungan impuls (\(I\))dan momentum (\(p\)), yaitu:
\(I = F.\Delta t = \Delta p\) \(\Rightarrow p = m.v\)
\(F.\Delta t = m.(v_t - v_0)\)
\(180\times 0,4 = 2.(v_t - (-20))\)
\(36 = v_t +20\)
\(v_t = 16\)
subtitusikan nilai \(v_t\) dan \(v-0\) ke persamaan (17.1), sehingga:
\(e = {-16\over -20} = 0,8\) \(\Rightarrow\) (Jawaban d.)
SOAL 18 SIMAK UI 2014/302/28
a. \({\pi \over 2} \sqrt{m\over 2k} + {3\pi \over 2} \sqrt{m\over 2k}\)
b. \({\pi \over 2} \sqrt{m\over k} + {3\pi \over 2} \sqrt{m\over 2k}\)
c. \({\pi \over 2} \sqrt{3m\over 2k} + {3\pi \over 2} \sqrt{m\over 2k}\)
d. \({\pi \over 2} \sqrt{2m\over k} + {3\pi \over 2} \sqrt{m\over 2k}\)
e. \({\pi \over 2} \sqrt{5m\over 2k} + {3\pi \over 2} \sqrt{m\over 2k}\)
Perhatikan gambar berikut!
Gambar (0), kondisi setimbang saat kedua tidak teregang dan tidak tertekan.
Gambar (1), kondisi saat beban M2 ditekan ke kiri. waktu t = 0 dimulai tepat saat beban M2 dilepaskan. beban M2 bergerak ke kanan. Sementara selama M2 bergerak menuju titik setimbang, beban M1 (cenderung ke kiri namun karena tertahan dinding membuatnya) tetap diam.
Gambar (2): balok M2 tepat sampai di titik setimbang. Saat ini pula balok M1 mulai bergerak ke kanan terhadap dinding (ke kiri terhadap pegas). Waktu dari kondisi (1) ke (3) adalah:
\(t_1 = {T \over 4}\),
di mana,
\(T = {2\pi \sqrt{m\over k}}\)
sehingga.
\(t_1 = {{\pi \over 2} \sqrt{m\over k}}\)
Gambar (3): Beban M1 dan M2 tepat berada pada posisi terjauh satu sama lain. karena keduanya sama-sama bergerak/bergetar, diasumsikan terdapat dua buah pegas sama panjang dengan pusat massa (lingkaran merah) sebagai ujung-ujungnya. konstanta gayanya menjadi k', di mana:
\({1\over k} = {1\over k'} + {1\over k'}\)
\(\Rightarrow k' = 2k\)
Waktu dari kondisi (2) ke (3) adalah \(t_2 = {T' \over 4}\),
di mana,
\(T' = {2\pi \sqrt{m\over 2k}}\)
sehingga.
\(t_2 = {{\pi \over 2} \sqrt{m\over 2k}}\)
Kondisi (4): Beban M1 dan M2 tepat berada pada posisi terdekat satu sama lain pertama kali. Waktu dari kondisi (3) ke kondisi (4) adalah \(t_3 = {T' \over 2}\), atau
\(t_3 = {\pi \sqrt{m\over 2k}}\)
Dengan demikian waktu untuk kedua benda terdekat pertama kali setelah M2 dilepaskan adalah:
\(t = t_1 + t_2 + t_3\)
\(t = {2\pi \sqrt{m\over k}} + {{\pi \over 2} \sqrt{m\over 2k}} +{\pi \sqrt{m\over 2k}}\)
\(t = {\pi \over 2} \sqrt{m\over k} + {3\pi \over 2} \sqrt{m\over 2k}\) \(\Rightarrow\) (Jawaban b.)
Soal 19. SIMAK UI 2018/31
Andaikan semua planet dalam tata surya mengalami pergantian musim seperti halnya yang ada di Bumi. Planet yang pergantian musimnya paling cepat adalah ....
a. Saturnus d. Bumi
b. Neptunus e. Merkurius
c. Mars
Penyelesaian.
waktu suatu musim kembali aktif di Bumi secara-rata adalah sekitar satu tahun ini sama dengan waktu revolusi Bumi terhadap matahari. Artinya waktu pergantian musim suatu planet dipengaruhi oleh waktu periode revolusi planet tersebut terhadap matahari.
planet mengorbit mengellilingi Matahari dikarenakan gaya gravitasi. Karena gerakannya melingkar mengelilingi Matahari, gaya gravitasi berperan sebagai gaya sentripetal.
Fg = Fsp
\({G.M.m\over r^2} = {m.r.\omega^2}\) .... (19.1)
di mana;
\(G = 6,67 \times 10^{-11}\) N.m2.kg-2
\(M =\) massa matahari (kg)
\(m =\) massa planet (kg)
\(r =\) jari-jari orbit (m)
\(\omega = {2\pi\over T} \)
dari persamaan (10.1), diperoleh persamaan periode revolusi yaitu:
\(T = 2\pi \sqrt{r^3\over G.M}\) (19.2)
Berdasarkan persamaan (19.2), menunjukkan bahwa di antara kelima planet yand diberikan, planet merkurius-lah yang memiliki waktu pergantian musim paling cepat, dikarenakan jarak ke matahari paling dekat (sehingga periode revolusinya paling singkat. \(\Rightarrow\) (Jawaban e.)
Soal 20. SIMAK UI 2015/10001/30
Suatu pabrik per membuat kurva karakteristik produknya seperti pada gambar di atas. Jika dianggap \(F_3 =\) 18 N, \(F_1 =\) 6 N dan energi potensial pegas pada saat per memanjang sebesar 0,04 m adalah 4,8 × 10\(^{-1}\) Joule, jarak antara posisi ∆x3 dan ∆x1 sebagaimana diberikan pada kurva karakteristik di atas adalah …. cm
a. 1 d. 4
b. 2 e. 5
c. 3
a. 1 d. 4
b. 2 e. 5
c. 3
Penyelesaian.
Diketahui:
\(F_3 =\) 18 N, \(F_1 =\) 6 N
\(EP = 4,8 × 10^{-1} \) J \(\Rightarrow \Delta x = 4 × 10^{-2}\) m
Ditanyakan:
\(|\Delta x_3 - \Delta x_1| =\) ….?
Jawab: (soal elatisitas)
Dengan menggunakan hukum hooke didapatkan bahwa
\(\Delta x = {F \over k}\), sehingga:
\(|\Delta x_3 - \Delta x_1| ={F_3 \over k} - {F_1 \over k}\) …. (20.1)
Untuk nilai \(k\) diperoleh dari energi potensial pegas, yaitu:
\(EP = {1\over 2}.k.(\Delta x)^2\)
\(k = {2.EP \over (\Delta x)^2}\)
\(k = {2 × 4,8 × 10^{-1} \over (4 × 10^{-2})^2}\)
\(k = {96 × 10^{-2} \over 16 × 10^{-4}}\)
\(k = 600\) N/m
Subtitusikan nilai \(k\) ke persamaan (20.1), sehingga:
\(|\Delta x_3 - \Delta x_1| ={18 \over 600} - {6 \over 600}\) m
\(|\Delta x_3 - \Delta x_1| =3 – 1 = 2\) cm \(\Rightarrow\) (Jawaban b.)