Hukum Hooke Pada Pegas
Perhatikan gambar berikut!
 |
| Sebuah pegas bertambah panjang sejauh \(\Delta L\) saat ditarik oleh suatu gaya sebesar \(F\) |
Menurut
hukum Hooke, dalam batas elastisitasnya, besar gaya luar \(F\) yang
bekerja pada suatu pegas sehingga pegas memendek atau memanjang sejauh
\(\Delta L\) dapat dinyatakan dengan rumus :
\(F = k.\Delta L\) .....(3)
Dengan : \(F\) = gaya luar pada pegas (N), \(k\) = konstanta gaya/elastis pegas N.m\(^{-1}\), \( \Delta L \) = perubahan panjang (m).
Contoh Hukum Hooke:
Sebuah
pegas memiliki konstanta gaya 200 N/m. Jika pegas ditarik dengan gaya
10 N, berapakah perubahan panjang yang dialami pegas tersebut .....?
Diketahui:
\(k = 200 \) N/m, \(F = 10 \) N
Ditanyakan:
\( \Delta L = ....?\)
Jawab:
\(F = k.\Delta L\) \(\Rightarrow\) \(\Delta L = {F \over k}\)
\(\Delta L = {10 \over 200} = {1 \over 20} = 0,05 \) m
\(\Delta L =5 \) cm
\(\Delta L = {10 \over 200} = {1 \over 20} = 0,05 \) m
\(\Delta L =5 \) cm
Menentukan Konstanta Gaya Pengganti Pada Susunan Pegas Seri
Perhatikan Gambar susunan seri dari tiga buah pegas di bawah ini.
Beberapa
pegas yang disusun seri seperti gambar di atas, dapat digantikan dengan
satu konsep pegas pengganti dengan nilai konstanta gaya dapat
dinyatakan sebagai berikut:
| \({1 \over k_s} = {1 \over k_1} +{1 \over k_2} + .... +{1 \over k_n}\) .....(4) |
Dengan \(k_s\) = konstanta pegas pengganti susunan seri N.m\(^{-1}\), \(k_1\) = konstanta pegas pertama, \(k_2\) = konstanta pegas kedua, demikian seterusnya hingga konstanta pegas ke \(n\) (\(k_n\)).
Contoh Soal 1 Susunan Pegas Seri:
Terdapat Tiga buah pegas dengan konstanta gaya berturut-turut 400 N/m, 600 N/m, 1200 N/m. Jika ketiganya disusun seri maka berapakah konstanta pegas penggantingya ....?
Diketahui:
\(k_1 = 400\) N/m, \(k_2 = 600\) N/m, \(k_3 = 1200\) N/m
Ditanya:
\(k_s = .....?\)
Jawab:
\({1 \over k_s} = {1 \over k_1} +{1 \over k_2} + {1 \over k_3}\)
\({1 \over k_s} = {1 \over 400} +{1 \over 600} + {1 \over 1200}\)
\({1 \over k_s} = {{3 + 2 +1} \over 1200} = {6 \over 1200}= {1 \over 200}\)
\({1 \over k_s} = {1 \over 200}\)
\( k_s = 200 \) N/m
\({1 \over k_s} = {{3 + 2 +1} \over 1200} = {6 \over 1200}= {1 \over 200}\)
\({1 \over k_s} = {1 \over 200}\)
\( k_s = 200 \) N/m
Menentukan Konstanta Gaya Pengganti Pada Susunan Pegas Paralel
Perhatikan Gambar susunan paralel dari tiga buah pegas di bawah ini.
Beberapa
pegas yang disusun paralel seperti gambar di atas, dapat digantikan dengan
satu konsep pegas pengganti dengan nilai konstanta gaya dapat
dinyatakan sebagai berikut:
| \(k_p = k_1 + k_2 + .... + k_n\) .....(5) |
Dengan \(k_p\) = konstanta pegas pengganti susunan paralel N.m\(^{-1}\), \(k_1\) = konstanta pegas pertama, \(k_2\) = konstanta pegas kedua, demikian seterusnya hingga konstanta pegas ke \(n\) (\(k_n\)).
Contoh Soal 2 Susunan Pegas Paralel:
Terdapat tiga buah pegas dengan konstanta gaya berturut-turut 400 N/m, 600 N/m, 1200 N/m. Jika ketiganya disusun paralel maka berapakah konstanta pegas penggantingya ....?
Diketahui:
\(k_1 = 400\) N/m, \(k_2 = 600\) N/m, \(k_1 = 1200\) N/m
Ditanyakan:
\(k_p = ....?\)
Jawab:
\(k_p = k_1 + k_2 + .... + k_n\)
\(k_p = 400 + 600 + 1200\)
\(k_p = 2200\) N/m
Contoh Soal 3 Susunan Pegas Gabungan
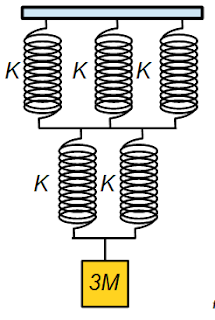
Perhatikan gambar sistem pegas berikut ini.
a. konstanta pegas pengganti
b. perubahan panjang total yang dialami sistem pegas tersebut.
Penyelesaian:
Diketahui:
\(k = 300\) N/m,
\(M = 240\) gr \(= 0,24\) kg.
a. Ditanyakan: \(k_t = ....?\)
Jawab:
Perhatikan gambar berikut:
Dengan bantuan gambar tersebut dapat ditentukan bahwa:
\(kp_1 = k + k + k = 3k\), dan \(kp_2 = k + k = 2k\), sehingga:
\({1 \over k_t } = {1 \over 3k} + {1 \over 2k} \)
\({1 \over k_t } = {{2 + 3} \over {6k}} = {5 \over 6k} \)
\(k_t = {6k \over 5}\)
\(k_t = {{6\times 300} \over 5} = {1800 \over 5}\)
\(k_t = 360\) N/m
b. Ditanyakan : \(\Delta L = ....?\)
subtitusikan nilai \(k = 300\) N/m. pada rumus \(k_t\) tersebut, sehingga menjadi
\(k_t = {{6\times 300} \over 5} = {1800 \over 5}\)
\(k_t = 360\) N/m
Jawab: gunakan persamaan Hukum Hooke,
\(F = k.\Delta L\) \(\Rightarrow\) \(\Delta L = {F \over k}\)
di mana \(F\) = berat beban \(w\)
\(w = m.g = 3M.g = 3 \times 0,24 \times 10 \)
\(w = 7,2\) N
\(\Delta L = {7,2 \over 360}\)\(\Delta L = {7,2 \over {3,6 \times 10^2}}\)
\(\Delta L = 2 \times 10^{-2} = 0,02 \) m
\(\Delta L = 2 \) cm
\(\Delta L = 2 \) cm